- Registriert
- 23.03.2021
- Beiträge
- 1.799
- Reaktionen
- 2.385
Genau das gleiche passiert bei den Farben und erklärt den Farbkreis, der analog zum Quintenzirkel ist.

Und HAL9000 sprach: "Das Gespräch hat keinen Zweck mehr. Es führt zu nichts."
Folge dem Video um zu sehen, wie unsere Website als Web-App auf dem Startbildschirm installiert werden kann.
Anmerkung: Diese Funktion ist in einigen Browsern möglicherweise nicht verfügbar.
Genau das gleiche passiert bei den Farben und erklärt den Farbkreis, der analog zum Quintenzirkel ist.



Richtig ist, dass sich Licht und Schall mit Hilfe der Wellentheorie beschreiben lassen. Damit ist aber schon Schluß mit den Gemeinsamkeiten.
Ich weiß nicht, was du mit "Wellenlänge eines bestimmten Spektrums" meinst (das macht so keinen Sinn), vielleicht spielst du auf die Spektralfarben an. Also die sogenannten reinen Farben, wo Licht einer ganz bestimmten Wellenlänge emitiert wird. Beim Schall wären das analog Sinuswellen einer ganz bestimmten Wellenlänge. Die Benennung der Spektralfarben ist vollkommen willkürlich, und hat sich historisch eingebürgert, wobei es heute noch Meinungsverschiedenheiten gibt, ob fünf oder sechs Namen sinnvoll sind. Die Spektralfarben des sichtbaren Bereichs bilden aber ein Kontinuum, und Namen wie Blau, Gelb etc sind nichts weiter als eine grobe Charakterisierung eines ganzen Bereichs von Spektralfarben, die sich sichtbar unterscheiden.
Interessant wird es aber erst, wenn man sich klar macht, was passiert, wenn man solche reinen Farben (monochromatisches Licht) bzw reine Töne (Sinuswellen) mischt. In der Akustik entstehen dadurch Klangfarben bei gleichbleibendem Grundton, mehr oder weniger harmonisch oder unharmonisch empfunden, bis hin zum Geräusch ohne wahrnehmbaren Grundton, alles natürlich mit fließendem Übergang. Ganz besonders interessant sind Mischungen von Grundtönen, die als Intervalle oder Akkorde wahrgenommen werden.
Die Farbwahrnehmung kennt vergleichbare Phänomene nicht, eine Mischung von Farbreizen führt immer wieder zu einem Farbreiz. Wenn ich grünes und rotes Licht mische, dann bekomme ich kein irgendwie geartetes Muster, so dass ich die beiden Farben diskret wahrnehmen kann, sondern ich nehme die Mischung als Gelb wahr. Wenn es also um die Erkennung von Farben geht, wäre es billig, sich auf 6 oder 7 Spektralfarbtöne zurückzuziehen, und sowas als "Absolutseher" zu bezeichnen. Ein Absolutseher müsste schon genau das leisten, was auch behauptet wurde, nämlich in der Lage zu sein, einen gesehenen Farbton ohne direkten Farbvergleich (das wäre relatives Farbensehen) in einem Farbkatalog wie RAL oder andere aufzufinden. Hier werden aus dem dreidimensionalen Farbraum systematisch Farbtöne angeordnet, die den Farbraum möglichst gut abdecken. Das sind dann in der Regel 2000-2500 Farben. Von mir aus kann man eine Dimension, die Helligkeit rausnehmen (meist ca. 10 Stufen), dann landet man bei 200-250 Farbtönen. Wenn die jemand erkennen und benennen kann, dann wäre der Begriff "Absolutseher" angebracht.
Und dabei belasse ich es jetzt, und danke für die Aufmerksamkeit, obwohl es mit Klavierspielen nix zu tun hat.
Das Gehirn (nicht nur das menschliche) ist ein Triangulationsmeister ... keine Laufzeitveränderung gibt es nur, wenn eine Geräuschquelle zu beiden Ohren den gleichen Abstand hat ... und dann hat man die Richtung, denn solche Dinge befinden sich IMMER auf der Ebene, welche ortogonal zur Hörachse verläuft. Jede Geräuschquelle ausserhalb dieser Ebene wird an zwei Ohren unterschiedlich registriert.Oben/Unten führt da dann zu keinen Laufzeitunterschieden.
Bei von Geburt an Blinden entwickelt sich auch sehr schnell das räumliche Gehör - zu wissen wie weit genau das Geräusch entfernt ist, ist da Überlebenswichtig.... es ist ja auch egal, wie das genau funktioniert, solange man nur weiß, wo ein Jäger oder das Frühstück sich befinden.
Das ist wieder Unsinn. Nicht nur ergibt die -willkürlich - gewählte, und im Profibereich nicht ausreichende Farbtiefe von 24Bit 16,7Mio Farben. Auch kann man nur diskrete Anzahlen von Elementen "unterscheiden". Leider enthält der hörbare Bereich des Schalls unendlich viele Frequenzen: 440Hz ist nicht 440,5Hz. Wo ziehst du die Grenze?Ein absoluter Absolutfarbseher müßte das ganze Spektrum des Bildschirmes von 18,7 Millionen Farben erkennen - genau so wie nach meiner Definition ein Absoluthörer ALLE für den Menschen hörbare Frequenzen unterscheiden müßte.
Beim Unterschied von 1 Hz.Wo ziehst du die Grenze?
Orientiere dich doch lieber an Cent.Beim Unterschied von 1 Hz.
Richtig, die Ebene, auf der die Schallquelle liegt, kann auf diese Weise herausgefunden werden. Aber noch nicht die Richtung / Lage innerhalb dieser Ebene. Also, die Katze (wenn sie den Kopf noch nicht gedreht hat) kann dann erstmal nicht feststellen, ob die Schallquelle in der Horizontalen (d.h. vor ihr oder hinter ihr) liegt oder eben von oben / unten was kommt.Das Gehirn (nicht nur das menschliche) ist ein Triangulationsmeister ... keine Laufzeitveränderung gibt es nur, wenn eine Geräuschquelle zu beiden Ohren den gleichen Abstand hat ... und dann hat man die Richtung, denn solche Dinge befinden sich IMMER auf der Ebene, welche ortogonal zur Hörachse verläuft. Jede Geräuschquelle ausserhalb dieser Ebene wird an zwei Ohren unterschiedlich registriert.


Richtig, es wird nicht im Sinne einer Formel berechnet, sondern ist eingeübt. Das Gehirn nähert Formeln sozusagen durch Mustererkennung an. Die Grundstrukturen (Neuronen und Synapsen) sind von Anbeginn an vorhanden, die entsprechende Verdrahtung, die dann diesen "Service" des Richtungshören anbietet, wird durch tausende von Auswertungen, wo Greifen, Sehen und Hören bzgl. Richtung aufeinander abgeglichen werden, antrainiert (vermute ich mal, da könnten wohl forschende Neurologen mehr dazu sagen)Solche Berechnungen führt unser Gehirn ständig aus ... und das ist keine humanoide Besonderheit, denn das machen nichtmal nur Säugetiere so.
Eine echte "Berechnung" (im mathematischen Sinne) ist es aber auch nicht ... vielen Tieren dürfte garnicht bewusst sein, was sie da tun ... es ist ja auch egal, wie das genau funktioniert, solange man nur weiß, wo ein Jäger oder das Frühstück sich befinden.
Die unter uns, die hören, machen das ja nicht erst seit Gestern ... im Grunde ist das Hören einer der ersten Sinneseindrücke, die ein Kind wahrnimmt ... früher sind nur die Reize des Tastsinns (beides wird bereits pränatal erfahren ... und damit auch geübt).@Häretiker Sehr interessant, wusste ich noch nicht. Das funktioniert aber nur, wenn für die Klangfarbe eine Referenz zur Verfügung steht, oder?
@Häretiker Sehr interessant, wusste ich noch nicht. Das funktioniert aber nur, wenn für die Klangfarbe eine Referenz zur Verfügung steht, oder?
Der erste Hund meiner Eltern machte um jede Kuhwiese einen großen Bogen ... oder blieb einfach stehen, wie angenagelt, wenn er keinen Bogen machen konnte (und einen ausgewachsenen Labradorrüden zieht man auch nicht mal eben hinter sich her).Ich kenne die Kuhglocken nur aus dem Urlaub, konnte aber immer sagen, wo die Kühe ungefähr sind. Dafür haben die ja die Dinger.

Wenn du wirklich von einem Synth "neue Klänge" hören willst, dann muss es schon ein "multi"-modularer Analogsynth (jedes Bauteil mindestens 20 mal vorhanden) mit Patchbay wie in alten Telefonzentralen sein.Außer, ich will einen Synth kaufen, dann versprechen mir das alle Hersteller. Seit 40 Jahren oder so.

Das zumindest ist einfach zu erklären.[[Warum man ein Klavier nicht einfach durchgängig so stimmen kann, dass alle denkbaren Quinten (nur als Beispiel) auch wirklich reine Quinten sind, habe ich immer noch nicht begriffen. Aber mir fehlt da einfach das Grundwissen. Von daher akzeptiere ich jetzt einfach die Tatsache, dass ein Klavier anscheinend immer einen nicht ganz reinen Klang hat. - Aber wenn's beim Cello klappt, warum klappt's dann beim Klavier nicht?]]
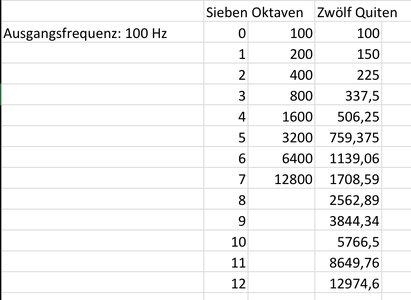
also ich find's gut erklärt.Haut‘s mir ruhig um die Ohren,

