Hier nur mal ein Zwischenbericht meines Vorankommens bei der Analyse vom Klavierton, den
@andreg freundlicherweise eingestellt hat. Wie nicht anders vorausgeahnt, sicher auch von euch, zieht sich das alles länger hin, ich mache das schließlich in meiner Freizeit und kann nur am Tag im Durchschnitt eine halbe Stunde dem Projekt opfern, zumal die eigentlichen Übungen im echten Klavierspiel mindestens genauso viel an Zeit und Aufmerksamkeit abbekommen sollen. Prinzipiell funktioniert meine Soundanalyse schon ganz gut, und ich weiß, wo ich hin will und mir dämmern die weiteren Herausforderungen.
Ich habe mal eben einen ganz einfachen Sound aus fünf Teiltönen gestrickt; wie er klingt, soll keine Rolle spielen, er ist rein willkürlich designed und hat selbst für mich genau nix mit einem Klavierklang zu tun. (Höre Anhang, falls interessiert, aber kein Wort zur Klangqualität.)
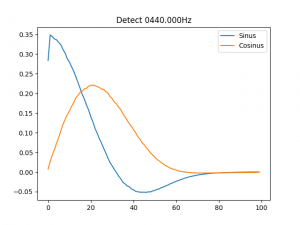
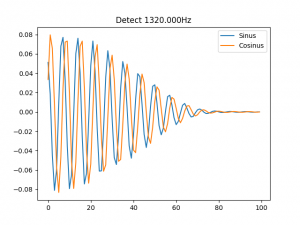
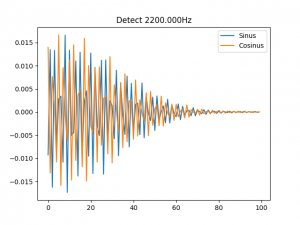
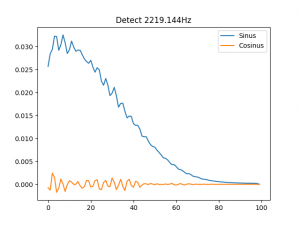
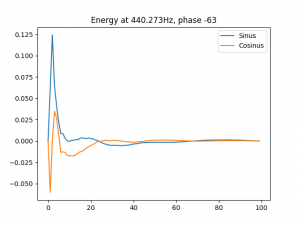
Zu jedem Teilton kenn ich die genauen Eigenschaften wie Frequenz, Maximalamplitude und Amplitudenverlauf. Ich kann meinem Programm also die generierte Sounddatei als Eingabe kredenzen, zusammen mit den Eigenschaften eines Teiltons, aus denen die Probe erstellt wird, um diese mit dem Eingangssignal multipliziert und intervallweise zu mitteln. Hier die Ergebnisse vom ersten Teilton:
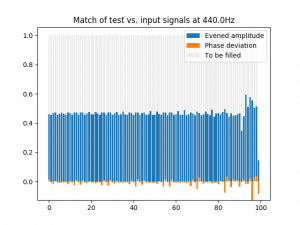
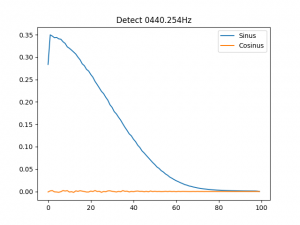
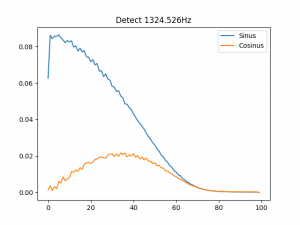
Wir sehen ein deutliches Rechteck (den Abweichungen vom idealen Rechteck muss ich noch auf den Grund gehen, ich tippe auf mathematische Ungenauigkeiten), geformt aus gleich hohen Säulen, das indiziert, dass ein Teilton mit den angegebenen Eigenschaften im Klang enthalten ist. Spaßeshalber werde ich mich mal bei der Frequenz des Teiltons um 1Hz vertun, dann würde das so aussehen:
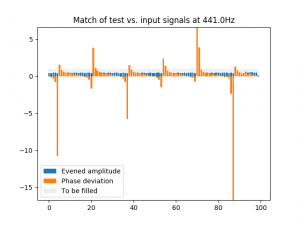
Hieran sieht man deutlich, dass die Balken der Phasenabweichung rhythmisch ausschlägt.
Würde man das Ursprungssignal und die sogenannte Probe übereinanderlegen und sich das Ergebnis anhören, würde man Schwebungen hören.
Diese Phasenabweichung wird bei der konventionellen Fast-Fourier-Transformation sehr früh wegabstrahiert. Wir brauchen sie, deshalb hilft uns FFT nicht weiter. Die Summe der absoluten Höhen der orangefarbenen Balken dient als Divisor, teilt die Summe der blauen Balken, die ideal die ganze Amplitude repräsentieren.
Und dann ist es ein leichtes, automatisiert alle Frequenzen abzutasten, erst im Bereich 400-500 – weil ich als Benutzer des Programms den Klang vorher mit einem bewährten einen FFT analysiert habe, und der in dem Bereich grob ein Maximum verortet – dann im Bereich 400-450, dann 425-450, dann 437.5-450, dann 437.5-443.75, und so weiter, der Algorithmus sucht auf diese Weise nach dem Maximum dieses Quotienten, also nach der Frequenz, bei der die blauen Balken insgesamt möglichst groß und die orangefarbenen Balken insgesamt möglichst klein sind.
Von den Frequenzen dieser Teiltöne kann ich schließen auf die Oktavstreckung und auf die Differenzen der Teiltonfrequenzen zur natürlichen Obertonreihe, die sich wegen der Seitensteifheit ergeben. Und ich kann
@andreg ggf. sagen, wenn sein Klavier verstimmt ist. ;)
Aber da ich bei einem unbekannten Sound den Amplitudenverlauf nicht kenne, kann ich auch nichts sagen über Attack, Sustain, und Release. Ich muss also zunächst pro forma davon ausgehen, dass die Amplitude ideal konstant ist, und der graue Bereich im Graph wird alles andere als gleich hoch. Ich bekomme für jeden der 100 Balken eine genaue negative Dezibelzahl und kann diesen Verlauf dann zu einer Kurve abstrahieren.
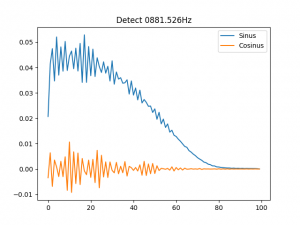
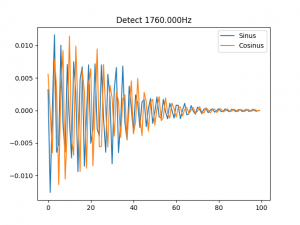
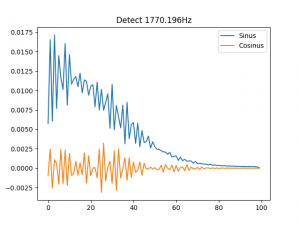
Aber auch hier wieder: Widdewiddewiddewitt ... die reale Physik wird mir noch ein ums andere Mal die lange Nase machen. Schauen wir uns zum Schluss mal den fünften Teilton meines Ad-Hoc-Sounds an, dessen Eigenschaften ich natürlich ebenso kenne und ich überprüfen kann, das sie im Gesamtklang enthalten sind:
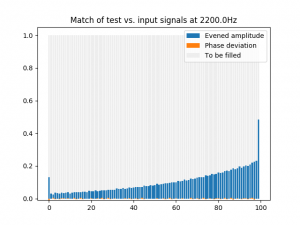
Rechteck? Pustekuchen. Ich erinnere mich, dass ich den Klang so gestaltet habe, dass sich Teiltöne mit steigender Ordnungszahl 1-5 zunehmend länger halten. Folglich hat der #5 zunehmend mehr Gewicht. Aber warum nimmt dann #1 nicht ab. Diesen Fragen muss ich noch nachgehen.
Es ist noch ein weiter Weg. Aber wenigstens muss ich euch nicht mehr mit meinen Pikometerschrittchen belästigen, sondern kann mir selber die Frage beantworten, wie nah mein generierter Sound soweit objektiv messbar schon dran ist an der Aufnahme von
@andreg.
Viele Grüße, und allen, ob sie nun an meinem Projekt interessiert sein mögen oder nicht, ein frohes, gesundes neues Jahr.


 ...
...  ... Gute Ergebnisse gibt es erst mal nicht, denn ich mach mal ne Pause von dem Projekt "Klavierklang nachbilden". Hörproben mag ich hier auch nicht mehr posten, selbst wenn ich mich wieder dran setze denn ihr habt mich überzeugt, dass ich hier wohl nie anderes zu lesen kriege als "ist kein Klavier". Lieber üb ich echtes Klavier, davon hab ich mehr auf lange Sicht.
... Gute Ergebnisse gibt es erst mal nicht, denn ich mach mal ne Pause von dem Projekt "Klavierklang nachbilden". Hörproben mag ich hier auch nicht mehr posten, selbst wenn ich mich wieder dran setze denn ihr habt mich überzeugt, dass ich hier wohl nie anderes zu lesen kriege als "ist kein Klavier". Lieber üb ich echtes Klavier, davon hab ich mehr auf lange Sicht.